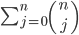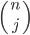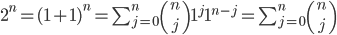Summing the Multinomial Coefficients

Posted on by

The sum of binomial coefficients \sum_{j=0}^n {n \choose j} equals 2n, because {n \choose j} is the number of ways to pick j elements from a set of size n, and 2n is the size of the powerset, the set of all subsets, of a set of size n: the sum, over all subset sizes, of the number of ways to choose subsets of a given size, is equal to the number of subsets. You can also see this using the binomial theorem itself:

2^{n} = (1 + 1)^{n} = \sum_{j=0}^{n} {n \choose j} 1^{j}1^{n-j} = \sum_{j=0}^{n} {n \choose j}

But of course there's nothing special about two; it works for multinomial coefficients just the same. The sum, over all m-tuples of subset sizes, of the number of ways to split a set of size n into subsets of sizes given by the m-tuple, is equal to the number of ways to split a set of size n into m subsets (viz., mn).

Moral Mechanism

Posted on by

It feels immoral to even think of using techniques to motivate oneself; one should instead just use one's free will to choose the correct action. How utterly degrading it would be, how insulting to the very notion of human dignity, to stoop to the level of contemplating one's own psychology using mere cause-and-effect reasoning, as if one were some sort of animal, or a machine!

But this moralizing is itself immoral, because it doesn't work. If I'm not smart enough to do the right thing for the right reasons, then I might at least aspire to do the right thing for the wrong reasons for the right reasons.

Straight Talk About Precompactness

Posted on by

So we have this metric space, which is this set of points along with a way of defining "distances" between them that behaves in a basically noncrazy way (points that are zero distance away from "each other" are really just the same point, the distance from one to the other is the same as the distance from the other to the one, and something about triangles).

Let's say (please, if you don't mind) that a sequence of points (xn) in our space is fundamental (or maybe Cauchy) iff (sic) for all positive ε, there's a point far enough along in the sequence so that beyond that point, the distance from one point to the next is less than ε. Let's also agree (if that's okay with you) to say that our metric space is sequentially precompact iff every sequence has a fundamental subsequence. If, furthermore, the precompact space is complete (all fundamental sequences actually converge to a point in the space, rather than leading up to an ætherial gap or missing edge), then we say it's compact. It turns out that compactness is an important property to pay attention to because it implies lots of cool stuff: like, compactness is preserved by homeomorphisms (continuously invertible continuous maps), and continuous functions with compact domains are bounded, and probably all sorts of other things that I don't know (yet). I'm saying sequentially precompact because I'm given to understand that while the convergent subsequences criterion for compactness is equivalent to this other definition (viz., "every open cover has a finite subcover") for metric spaces, the two ideas aren't the same for more general topological spaces. Just don't ask me what in the world we're going to do with a nonmetrizable space, 'cause I don't know (yet).

But anyway, as long as we're naming ideas, why not say that our metric space is totally bounded iff for every ε, there exists a finite number of open (that is, not including the boundary) balls that cover the whole space? We can call the centers of such a group of balls an ε-net. Our friend Shilov quotes his friend Liusternik as saying, "Suppose a lamp illuminating a ball of radius ε is placed at every point of a set B which is an ε-net for a set M. Then the whole set M will be illuminated." At the risk of having names for things that possibly don't actually deserve names, I'm going call each point in an ε-net a lamp. Actually Shilov, and thus likely Liusternik, is talking about closed balls of light around the lamps, not the open ones that I'm talking about. In a lot of circumstances, this could probably make all the difference in the world, but for the duration of this post, I don't think you should worry about it.

But this fear of having too many names for things is really a very serious one, because it turns out that sequential precompactness and total boundedness are the same thing: not only can you not have one without the other, but you can't even have the other without the one! Seriously, like, who even does that?!

Continue reading →

On Arc Length

Posted on by

Zeno knew, but did not know enough; a minute is divided
Into fragments, and each fragment sees, for points it o'er presided:
A small change, of which I take the distance
Along each fragment's lost existence:
The root of the sum of the squares
Of the length and the width and the height
Of the change in the range as the fragment is spanned
As the fragment is stricken from sight!

Mathematics Is the Subfield of Philosophy That Humans Are Good At

Posted on by

By philosophy I understand the discipline of discovering truths about reality by means of thinking very carefully. Contrast to science, where we try to come up with theories that predict our observations. Philosophers of number have observed that the first ten trillion nontrivial zeros of the Riemann zeta function are on the critical line, but people don't speak of the Riemann hypothesis as being almost certainly true, not necessarily because they anticipate a counterexample lurking somewhere above ½ + 1026i (although "large" counterexamples are not unheard-of in the philosophy of numbers), but rather because while empirical examination is certainly helpful, it's not really what we do. Mere empiricism is usually sufficient for knowing (with high probability) what is true, but as philosophers, we want to explain why, and moreover, why it could not have been otherwise.

When we try this on topics like numbers or shapes, it works really, really well: our philosophers quickly reach ironclad consensuses about matters far removed from human intuition. When we try it on topics like justice or existence ... it doesn't work so well. I think it's sad.

Contemporary

Posted on by

I've been taking a summer course at a university which I won't name, because whenever I do, I'm always tempted to replace one of the words with an obscenity that starts with the same letter, which is probably a bad habit. The topic is contemporary sexuality, which seemed like a fine choice for knocking out one of my remaining so-called "general education" requirements, and maybe even learning something relevant to my interests.

The class ends on Thursday the ninth, and I had intended to make a lot of progress today (the sixth) filling out the workbook (worth half a letter grade) due then. I didn't get very far. The task shouldn't be difficult; my goal is only to reduce the probability of my receiving a C in the class by means of circling the appropriate letters for the multiple-choice prompts (for which the answers are conveniently provided) and scribbling responses to the short-answer questions, glancing at the reading as necessary. There was once a time when I would have regarded this behavior as sinful: of course what you're supposed to do is carefully do the corresponding reading by the assigned date before thoughtfully filling out each workbook section, only using the multiple-choice answers to check your work. But if I've abandoned my moral scruples sometime in the past five years, then I also throw far fewer crying fits, and I don't think these changes are unrelated.

Continue reading →

Lies and Delusion

Posted on by

One day, two philosophers were dining in a restaurant. "There's no such thing as lying," said the first philosopher to his companion. "Anytime someone speaks falsehood, it must be the case that they are merely deluded, or that part of them is, for the love of truth is so essential to the nature of agency that the very notion of deception is repugnant to it."

"On the contrary, there's no such thing as delusion," said the second philosopher. "Anytime someone thinks falsehood, it must be the case that they are merely lying, or that part of them is, for the perception of truth is so essential to the nature of agency that the very notion of misapprehension is repugnant to it."

A waitress, overhearing this exchange, found that she did not want to restrain herself. "You're both lying!" she shouted at the philosophers. "Stop lying!"

An Idea for a Psychology Experiment

Posted on by

Let me know if someone's actually done this.

Experiment: Use undergraduate schoolstudents as test subjects. Give each subject a shuffled deck of playing cards and ask them to sort it by suit and rank as quickly as possible. Time how long each subject takes to complete the task.

Prediction: A minority of computer science students will markedly outperform everyone else.

The Morality of Ringing a Bell

Posted on by

"Synthia, I want your opinion on something," said Quiana.

"You will have it."

"Is it wrong to enjoy ringing a bell?"

"Pardon me?" said Synthia.

"I said," said Quiana, "is it wrong to enjoy ringing a bell?"

"I heard you the first time," said Synthia irritably, "but I presume the question is prompted by some context you have not yet told me, a context I would need to know to provide you with the best answer I can give."

Continue reading →

The Problem With My Friend Who Has This Problem

Posted on by

Dear reader, I have this ... friend, who has this problem, and I wanted to ask—

What do you mean, Who is he? You wouldn't know ... her, and—

You must realize that I'm already aware that it's a standard trope for someone to say "I Have This Friend" when they're really talking about themselves, and given that I know it's already a standard trope, I would never be so obvious as to actually do it! Therefore you must truthfully conclude that I really am talking about a—

Okay, that's a good point. No, I didn't consider the fact that that reasoning can't possibly be sound because if it were, then people would use it as an excuse to falsely claim that they were speaking about a friend rather than themselves, thereby contradicting the assumption that the reasoning is—

Well, we could try to calculate the probability that I really am talking about a friend conditional on your epistemic state and taking into account the game-theoretic considerations just mentioned, but that could take all night, so will you just listen to my transparent lies for fuck's sake?

Continue reading →

Training Your Very Own Turtle to Draw the Boundary of the Mandelbrot Set

Posted on by

Dear reader, I don't think I've ever told you how much I love the Python standard library, but I do. When they say "Batteries included," they may not mean it in the sense of "a device that produces electricity by a chemical reaction between two substances," but they do mean it in the sense of "an array of similar things," where the similar things are great libraries. If you need a CSV reader, it's there. If you need fixed-point decimal arithmetic, it's there. But although perhaps it should not have surprised me, never has my joy and appreciation been greater than the fateful moment when I learned that the standard library itself contains a module for

Continue reading →

Trying to Buy a Lamp

Posted on by

Dear reader, I had wanted to tell you an anecdote about a recent incident in which I considered myself to have been outrageously mistreated, but it occurred to me that you probably would not find the story at all worthy of note. In fact, I fear you would be quite likely to think less of me for complaining in such a melodramatic fashion about something which the prevailing norms of our Society consider quite ordinary and proper. And what authority do I have to insist that it's Society that is in the wrong, and not I?

So I won't tell you. Instead, let me tell you a completely unrelated anecdote about my analogue in an alternate universe not entirely unlike our own. You see, recently, my alternate-universe analogue wanted to buy a table lamp, so he went—or let us say in a manner of speaking that I went—to a store to purchase one.

In the showroom, I found a lamp I liked, flagged down a salesman, and said to him, "I'd like to buy this lamp."

"Have you previously purchased a side table from us before?" he said.

"No," I said, somewhat puzzled by the seemingly irrelevant question.

"Well, you can't buy a lamp unless you already have a table to put it on," said the salesman in a tone of polite condescension.

"Oh, I certainly agree that it simply wouldn't do to get a lamp without having a table to put it on," I said, "but you see, I already have a table."

"So you did buy a table from us."

"No," I said.

"So you don't have a table."

Continue reading →

Interpolating Between Vectorized Green's Theorems

Posted on by

Green's theorem says that (subject to some very reasonable conditions that we need not concern ourselves with here) the counterclockwise line integral of the vector field F = [P Q] around the boundary of a region is equal to the double intregral of \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y} over the region itself. It's natural to think of it as a special case of Stokes's theorem in the case of a plane. We can also think of the line integral as the integral of the inner product of the vector field with the unit tangent, leading us to write Green's theorem like this:

\oint_{\partial D}\vec{\mathbf{F}}\cdot\vec{\mathbf{T}}\, ds=\iint_{D}(\mathrm{curl\,}\vec{\mathbf{F}})\cdot\vec{\mathbf{k}}\, ds

But some texts (I have Mardsen and Tromba's Vector Calculus and Stewart's Calculus: Early Transcendentals in my possession; undoubtedly there are others) point out that we can also think of Green's theorem as a special case of the divergence theorem! Suppose we take the integral of the inner product of the vector field with the outward-facing unit normal (instead of the unit tangent)—it turns out that

\oint_{\partial D}\vec{\mathbf{F}}\cdot\vec{\mathbf{n}}\, ds=\iint_{D}\mathrm{div\,}\vec{\mathbf{F}} ds

—which suggests that there's some deep fundamental sense in which Stokes's theorem and the divergence theorem are really just mere surface manifestations of one and the same underlying idea! (I'm told that it's called the generalized Stokes's theorem, but regrettably I don't know the details yet.)

Continue reading →