The sum of binomial coefficients 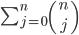$\sum_{j=0}^n {n \choose j}$ equals 2ⁿ, because 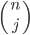${n \choose j}$ is the number of ways to pick j elements from a set of size n, and 2ⁿ is the size of the powerset, the set of all subsets, of a set of size n: the sum, over all subset sizes, of the number of ways to choose subsets of a given size, is equal to the number of subsets. You can also see this using the binomial theorem itself:

$$2^{n} = (1 + 1)^{n} = \sum_{j=0}^{n} {n \choose j} 1^{j}1^{n-j} = \sum_{j=0}^{n} {n \choose j}$$

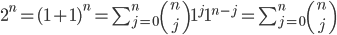
But of course there's nothing special about two; it works for multinomial coefficients just the same. The sum, over all m-tuples of subset sizes, of the number of ways to split a set of size n into subsets of sizes given by the m-tuple, is equal to the number of ways to split a set of size n into m subsets (viz., mⁿ).