Dear reader, I don't think I've ever told you how much I love the Python standard library, but I do. When they say "Batteries included," they may not mean it in the sense of "a device that produces electricity by a chemical reaction between two substances," but they do mean it in the sense of "an array of similar things," where the similar things are great libraries. If you need a CSV reader, it's there. If you need fixed-point decimal arithmetic, it's there. But although perhaps it should not have surprised me, never has my joy and appreciation been greater than the fateful moment when I learned that the standard library itself contains a module for

TURTLE GRAPHICS

Yes, turtle graphics! In case you had a deprived childhood, I should explain: the idea is that you have a cursor on the screen (the turtle), and you can type, say,

FORWARD 10

and then the turtle will move forward ten units, drawing a line as it goes. And then you can say, like,

RIGHT 60

and the turtle will rotate 60 degrees clockwise. What a glorious introduction to the idea of computing: the user has her very own turtle to command, in effect becoming a godlike master of turtle existence with power limited only by her imagination and the bounds on thought itself! Isn't that truly outrageous (truly, truly, truly outrageous)?!

No it's not, you say? Well, fair enough. It is only to be expected that we should grow jaded with small miracles as we gain experience, and maybe I should stop doing that thing where I pretend to be more enthusiastic about geeky things than I actually am in some pathetic and misguided attempt to signal intelligence and curiosity.

But in any case, as long as we have turtles, we might as well have them do something vaguely amusing. Like, let's say, drawing the edge of the Mandelbrot set? Sure, okay. Let's do it.

One thing you have to know about turtles is—well, it's probably not very polite to say this, but it needs to be said—they're not very bright. You can't just say, "Oh, turtle friend!—would you please be a dear and draw the boundary of the Mandelbrot set for me?" because they'd never figure out how to do that on their own. You've got to give them very specific instructions.

The other thing you have to know about turtles is that they don't speak English; you have to tell them what to do in their native language. Our particular turtle happens to speak Python.

Now we should be ready to proceed, except ... well, we've all seen the famous pictures of the Mandelbrot set, but how is it defined, anyway? Well, as the great Jonathan Coulton sings (slightly edited):

Just [let zee be zero] in the complex plane,
Let zee-one be zee-squared plus cee,
Zee-two is zee-one squared plus cee,
Zee-three is zee-two squared plus cee, and so on.
If the series of zees will always stay
Close to cee and never trend away,
That point is in the Mandelbrot set.

That is, we pick a number c in ℂ, iterate z_n+1 = z_n² + c starting from zero, and if the z_n diverge off to infinity, then that particular c is not in the Mandelbrot set.

Let's start writing instructions for our turtle. First, we'll summon the turtle. Also, let's tell her to look up instructions on how to compute the argument of a complex number—don't ask me how, but I have a feeling we're going to need that later:

import turtle
from cmath import phase

Now, it turns out (claims Wikipedia, and I believe it), that if the absolute value of one of our z_ns ever exceeds two, then that sequence will diverge. This seems like a useful fact, so let's tell our turtle how to calculate how many iterations it will take for the sequence associated with a particular c to exceed two, and if it doesn't do so within some given number of iterations, then to tell us that:

def z_n_escape_time(c, n):
    z = 0
    for i in range(n):
        z = z**2 + c
        if abs(z) > 2:
            return i
    return False

To approximate the boundary of the Mandelbrot set, we'll tell the turtle to consider a grid of reasonably-finely-spaced points, and to consider a point to be on the boundary if the number of iterations it takes for the sequence for that point to exceed two is in some given range. We'll also tell her to sort those points by their argument, because that seems like a somewhat-reasonable order to visit them in:

def mandelbrot_edge(resolution, iterations, edge):
    points = []
    x_coordinates = [-2+i*(3/resolution) for i in range(int(resolution*1.5))]
    y_coordinates = [1-j*(2/resolution) for j in range(resolution)]
    for x in x_coordinates:
        for y in y_coordinates:
            if z_n_escape_time(complex(x,y), iterations) in edge:
                points.append((x,y))
    points = sorted(points, key=lambda p: phase(complex(p[0],p[1])))
    return points

Then (choosing some reasonable-looking numbers as specific parameters for our earlier instructions) we tell our turtle to visit all those points, drawing along the way:

def draw_boundary(protagonist, boundary_points, speed):
    protagonist.speed(speed)
    protagonist.penup()
    protagonist.setheading(protagonist.towards(boundary_points[0][0],boundary_points[0][1]))
    protagonist.forward(protagonist.distance(boundary_points[0][0],boundary_points[0][1]))
    protagonist.pendown()
    for p in boundary_points[1:]:
        protagonist.setheading(protagonist.towards(p[0],p[1]))
        protagonist.forward(protagonist.distance(p[0],p[1]))

def main():
    setting = turtle.Screen()
    protagonist = turtle.RawTurtle(setting)
    protagonist.shape("turtle")
    points = [(190*p[0],190*p[1]) for p in mandelbrot_edge(300, 500, list(range(60,500)))]
    draw_boundary(protagonist, points, 10)
    setting.mainloop()

if __name__ == "__main__":
    main()

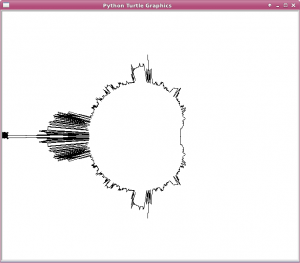
And we get this:

Okay, so it's not perfect. But give the turtle a little credit, maybe? She tried. We tried. And if that's not good enough—and, well, I guess it clearly is not good enough—then I can only beg for forbearance on the part of any powers that could save us from our imminent self-destruction, we wretched and miserable creatures that are good enough to try but not good enough to succeed.