Green's theorem says that (subject to some very reasonable conditions that we need not concern ourselves with here) the counterclockwise line integral of the vector field F = [P Q] around the boundary of a region is equal to the double intregral of 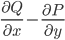$\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}$ over the region itself. It's natural to think of it as a special case of Stokes's theorem in the case of a plane. We can also think of the line integral as the integral of the inner product of the vector field with the unit tangent, leading us to write Green's theorem like this:

$$\oint_{\partial D}\vec{\mathbf{F}}\cdot\vec{\mathbf{T}}\, ds=\iint_{D}(\mathrm{curl\,}\vec{\mathbf{F}})\cdot\vec{\mathbf{k}}\, ds$$

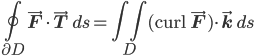
But some texts (I have Mardsen and Tromba's Vector Calculus and Stewart's Calculus: Early Transcendentals in my possession; undoubtedly there are others) point out that we can also think of Green's theorem as a special case of the divergence theorem! Suppose we take the integral of the inner product of the vector field with the outward-facing unit normal (instead of the unit tangent)—it turns out that

$$\oint_{\partial D}\vec{\mathbf{F}}\cdot\vec{\mathbf{n}}\, ds=\iint_{D}\mathrm{div\,}\vec{\mathbf{F}} ds$$

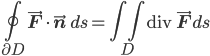
—which suggests that there's some deep fundamental sense in which Stokes's theorem and the divergence theorem are really just mere surface manifestations of one and the same underlying idea! (I'm told that it's called the generalized Stokes's theorem, but regrettably I don't know the details yet.)

Continue reading →

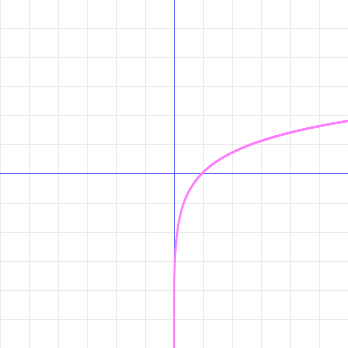
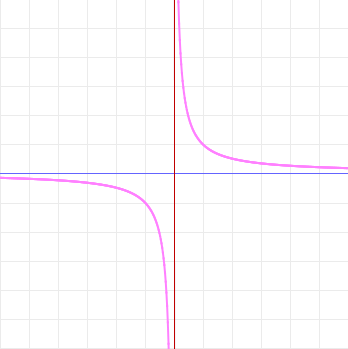
Most people learn during their study of the differential and integral calculus that the derivative of the natural logarithm ln x is the reciprocal function 1/x. Indeed, sometimes the natural logarithm is defined as 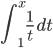$\int_1^x \frac{1}{t}\,dt$. However, on observing the graphs of ln x and 1/x, the inquisitive seeker of knowledge can hardly fail to notice a disturbing anomaly:

The natural logarithm is only defined for positive numbers; no part of its graph lies in quadrants II or III. But the reciprocal function is defined for all nonzero numbers. So (one cannot help oneself but wonder) how could the latter be the derivative of the former? If the graph of the natural logarithm isn't there to be differentiated in the left half of the plane, how could its derivative be defined in that region?
Continue reading →