baseball scorecard tablet app that downloads the official scorekeeper's version after the game and grades you on accuracy
Tag Archives: notation
Iff as Conditional Chain
I'm not sure I like how when we want to prove that two statements are equivalent, we typically say "A if and only if B" and we prove it by separately proving "both directions" A ⇒ B and B ⇒ A, but when we want to prove three or more statements are equivalent, we typically say "The following are equivalent" and prove a "circular chain" of conditionals (1) ⇒ (2) ⇒ [...] ⇒ (n) ⇒ (1), as if these were different proof strategies. Because really, the "both directions" business is just a special case of the chain-of-conditionals idea: (1) ⇒ (2) ⇒ (1). At the very least, one of my books ought to have mentioned this.
Subscripting as Function Composition
Dear reader, don't laugh: I had thought I already understood subsequences, but then it turned out that I was mistaken. I should have noticed the vague, unverbalized discomfort I felt about the subscripted-subscript notation, (ank). But really it shouldn't be confusing at all: as Bernd S. W. Schröder points out in his Mathematical Analysis: A Concise Introduction, it's just a function composition. If it helps (it helped me), say that (an) is mere syntactic sugar for a(n): ℕ → ℝ, a function from the naturals to the reals. And (ank) is just the composition a(n(k)), with n(k): ℕ → ℕ being a strictly increasing function from the naturals to the naturals.
Colon-Equals
Sometimes I think it's sad that the most popular programming languages use "=" for assignment rather than ":=" (like Pascal). Equality is a symmetrical relationship: "a equals b" means that a and b are the same thing or have the same value, and this is clearly the same as saying that "b equals a". Assignment isn't like that: putting the value b in a box named a isn't the same as putting the value a in a box named b!—surely an asymmetrical operation deserves an asymmetrical notation? Okay, so it is an extra character, but any decent editor can be configured to save you the keystroke.
I'd like to see the colon-equals assignment symbol more often in math, too. For example, shouldn't we be writing lower indices of summation like this?—
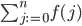
—the rationale being that the text under the sigma isn't asserting that j equals zero, but rather that j is assigned zero as the initial index value of what is, in fact, a for loop:
sum = 0;
for (int j=0; j<=n; j++)
{
sum += f(j);
}
return sum;