Should auld acquaintance be forgot and never brought to mind? Should auld acquaintance be forgot, and days of auld lang syne? (Hint: Assume the opposite and try to derive a contradiction.)
Monthly Archives: December 2011
Dialogue Concerning Birthdays
"Happy birthday, Synthia!"
"Why," mused Synthia, "do we celebrate birthdays? I fail to see anything special about the calendar day on which a person's age-in-calendar-years passes an integer. Are things supposed to be different now that it's been seven-point-five-seven-four times ten-to-the-eighth seconds since my birth, rather than seven-point-five-seven-three?"
Quiana suppressed a groan. Somehow she had been expecting Synthia to say something "normal," like Thanks! But knowing Synthia, it would have been unusual if she had done so: relative to Quiana's state of knowledge of her friend, this—the general style, though not, of course, the specific questions—was the normal response.
Continue reading
The Derivative of the Natural Logarithm
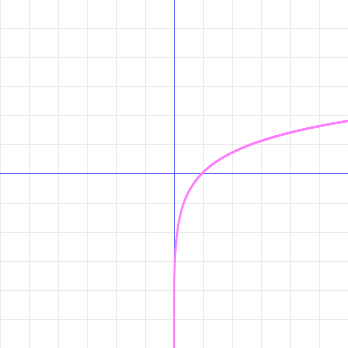
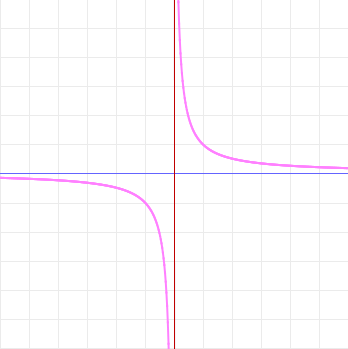
Most people learn during their study of the differential and integral calculus that the derivative of the natural logarithm ln x is the reciprocal function 1/x. Indeed, sometimes the natural logarithm is defined as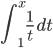 
. However, on observing the graphs of ln x and 1/x, the inquisitive seeker of knowledge can hardly fail to notice a disturbing anomaly:
The natural logarithm is only defined for positive numbers; no part of its graph lies in quadrants II or III. But the reciprocal function is defined for all nonzero numbers. So (one cannot help oneself but wonder) how could the latter be the derivative of the former? If the graph of the natural logarithm isn't there to be differentiated in the left half of the plane, how could its derivative be defined in that region?
Continue reading