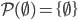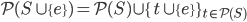Dear reader, as another year comes to a close, it is perhaps wise that we should take a few moments to reflect on what we learned here at An Algorithmic Lucidity in 2013—the year that was!
In the year 2013, this blog saw 103 posts and (at press time) 40 comments. Among these—
We heard a poem about why you should hire me. We surveyed a few numbers between 0 and 1. (Friend of the blog Grognor told me that the funniest part was the explicit disclaimer that the list was non-exhaustive. I replied that not everyone knows about the diagonalization argument—but considering this blog's, um, selective audience, maybe my readers do—all five of you!) We mentioned some hidden costs of talking about stuff. We noted that some words have substrings which are other words. I wrote a series about my experiences studying web development at App Academy (9 8 7 6 5 4 3 2 1). I pasted my first attempt at an OKCupid profile. We observed that I'm a moron. Books arrived in the post. We mused on the nature of personhood and implemented some classic algorithms: the Ford-Fulkerson technique somewhat clumsily in Ruby, quicksort in the form of a letter to a fictional horse, and Huffman coding in Python. We lamented the nature of existence, noticed the non-observance of an unusual tradition, and heard a poem about watching a motion picture by someone you met at university. Three problems with unsolicited advice were discussed, as was the role of bases in the theory of vector spaces, and the subjective indistinguishability of propaganda and other forms of instruction.