Most people learn during their study of the differential and integral calculus that the derivative of the natural logarithm ln x is the reciprocal function 1/x. Indeed, sometimes the natural logarithm is defined as 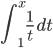$\int_1^x \frac{1}{t}\,dt$. However, on observing the graphs of ln x and 1/x, the inquisitive seeker of knowledge can hardly fail to notice a disturbing anomaly:

The natural logarithm is only defined for positive numbers; no part of its graph lies in quadrants II or III. But the reciprocal function is defined for all nonzero numbers. So (one cannot help oneself but wonder) how could the latter be the derivative of the former? If the graph of the natural logarithm isn't there to be differentiated in the left half of the plane, how could its derivative be defined in that region?

Some would-be explorers lose all hope or sanity in the face of such bizarre and inexplicable mysteries, but even those brave souls who manage to retain their wits are not guaranteed success: many (who can say but that most?) will die never knowing the answer. But not you, dear reader!—for in this very post, I will share with you the true secret of the derivative of the natural logarithm! Some people may find some of what I am about to say somewhat disturbing, even frightening. But if your love of truth exceeds your fear of the unknown, keep reading, and I will show you the strange world that lies beneath these familiar and seemingly innocent graphs.

You see, dear reader, the natural logarithm is not what we think it is. Your typical person-in-the-street hears talk of the natural logarithm and says, "Oh, sure, I know all about ln x; that's just the exponent you put on base e to get x." And, to be fair, it is. But it's also so much more! Ask our person-in-the-street what exponent you put on base e to get negative three, and no doubt she will regard you as mad. "Manifestly," we can imagine her replying, "manifestly there's no such thing. The exponential function e^x is always positive." And, to be fair, it is—if you arbitrarily restrict your mind to the mundane, oppressive, and boring magisterium of the so-called "real" numbers!

Probably the dear reader is already familiar with the numbers which are said to be complex, those of the form a + bi, where i is the square root of negative one. (To those who object that taking the square root of a negative number is a feat that simply cannot be done, the proper reply is only, "Watch me!") The reader may furthermore recall the Euler formula e^ix = cos x + isin x, source of the much-marveled-at identity e^πi = -1. With these prerequisites understood, it's quite reasonable to suspect that if we have a complex exponential, its inverse must be the complex logarithm, and that true apprehension of the nature of such is the key insight that will let us resolve the mystery at hand. And this does, in fact, turn out to be the case—but not so fast.

There is a difficulty here that must be explained. The dear reader may still yet furthermore recall that to say that a function is invertible is to say that it is both injective (which is to say that every element in the codomain is mapped to by at most one element in the domain, which is to say that distinct inputs have distinct outputs) and surjective (which is to say that every element in the codomain is mapped to by at least one element in the domain, which is to say that our codomain only includes actual outputs of our function). And dear reader, it turns out (to our great horror and distress) that the complex exponential is not injective! Was our dream of a complex logarithm nothing but a gaudy delusion?

On further consideration, however, it becomes clear that the situation is not so bad as all that. Probably the dear reader has faced analogous difficulties before. Recall that positive numbers actually have two square roots, a positive one and a negative one, and yet we casually designate the positive one as the principal square root, yielding us a square root function. We use a similar technique to define inverse trigonometric functions. Is it ugly? Yes. But does it work? Apparently.

So we can perform the same kind of surgical horror in order to get a proper function out of the complex logarithm idea: pick a ray emanating from the origin in the complex plane and cut the logarithm there—but I'll spare the dear reader the grisly details, which can be found in any standard text on complex analysis.

There is, however, another point of view. The reason a function needs to be injective in order to be invertible is because functions are defined such that each input has a unique output. There are reasons for defining it that way, but it is ultimately only a definition, a convention for what we mean when we use the world function, and mere definitions can't coerce true facts into being something other than what they are. Just because a non-injective function doesn't have an inverse function doesn't mean we can't talk about that-which-inverts-it; it only means that for clear communication, we should avoid calling the inverting-thing a function. Just call it a multifunction or a relation instead. (One can even imagine that if the history of mathematical inquiry had gone differently, we might call multifunctions functions and functions (say) deterministic functions, although some would argue that it is useless and idle to speculate about worlds that are not our own.)

So if we understand the complex logarithm multifunction as that-which-inverts the complex exponential, then we can understand the logarithm of a negative number -x₀ as ln x₀ + (2n+1)πi where n ∈ ℤ, because e^{ln x₀ + (2n+1)πi} = e^{ln x₀}e^(2n+1)πi = -e^{ln x₀} = -x₀.

But now we are ready to resolve the mystery that we set out to explain, of why the reciprocal function is the derivative of the natural logarithm even though no real number is the logarithm of a negative number, for now it is plain to see that the logarithm of a negative number is complex, but the derivative of the logarithm is real, because the imaginary part is a constant that drops out when we take the derivative:

$$f'(-x_0) = \lim_{h \to 0} \frac{f(-x_0+h)-f(x_0)}{h} = \lim_{h \to 0} \frac{(\ln{(x_0 - h)} + (2n+1)\pi i) - (\ln{x_0} + (2n+1)\pi i)}{h}$$

$$= \lim_{h \to 0} \frac{\ln{(x_0 - h)} - \ln{x_0}}{h}$$

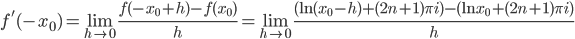
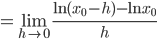
—which turns out to be -1/x₀, as expected.

Some might object that this argument is so sloppy as to be treacherous, misleading, and invalid: we've brazenly assumed that the definition of the derivative familiar from the study of the single-variable calculus can be applied to this complex-valued thing that isn't even a function, with no concern for preciseness, rigor, or even the Cauchy-Riemann conditions. But look. Presented with a procedure that makes sense and gives the right answer, perhaps the dear reader would be so kind as to cut me some goddam slack? I would be ever so much obliged.