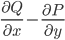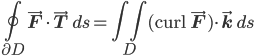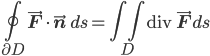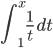So we have this metric space, which is this set of points along with a way of defining "distances" between them that behaves in a basically noncrazy way (points that are zero distance away from "each other" are really just the same point, the distance from one to the other is the same as the distance from the other to the one, and something about triangles).
Let's say (please, if you don't mind) that a sequence of points (xn) in our space is fundamental (or maybe Cauchy) iff (sic) for all positive ε, there's a point far enough along in the sequence so that beyond that point, the distance from one point to the next is less than ε. Let's also agree (if that's okay with you) to say that our metric space is sequentially precompact iff every sequence has a fundamental subsequence. If, furthermore, the precompact space is complete (all fundamental sequences actually converge to a point in the space, rather than leading up to an ætherial gap or missing edge), then we say it's compact. It turns out that compactness is an important property to pay attention to because it implies lots of cool stuff: like, compactness is preserved by homeomorphisms (continuously invertible continuous maps), and continuous functions with compact domains are bounded, and probably all sorts of other things that I don't know (yet). I'm saying sequentially precompact because I'm given to understand that while the convergent subsequences criterion for compactness is equivalent to this other definition (viz., "every open cover has a finite subcover") for metric spaces, the two ideas aren't the same for more general topological spaces. Just don't ask me what in the world we're going to do with a nonmetrizable space, 'cause I don't know (yet).
But anyway, as long as we're naming ideas, why not say that our metric space is totally bounded iff for every ε, there exists a finite number of open (that is, not including the boundary) balls that cover the whole space? We can call the centers of such a group of balls an ε-net. Our friend Shilov quotes his friend Liusternik as saying, "Suppose a lamp illuminating a ball of radius ε is placed at every point of a set B which is an ε-net for a set M. Then the whole set M will be illuminated." At the risk of having names for things that possibly don't actually deserve names, I'm going call each point in an ε-net a lamp. Actually Shilov, and thus likely Liusternik, is talking about closed balls of light around the lamps, not the open ones that I'm talking about. In a lot of circumstances, this could probably make all the difference in the world, but for the duration of this post, I don't think you should worry about it.
But this fear of having too many names for things is really a very serious one, because it turns out that sequential precompactness and total boundedness are the same thing: not only can you not have one without the other, but you can't even have the other without the one! Seriously, like, who even does that?!