[NOTICE: The conclusion of this post is hereby retracted because it turns out that the proposed definition of a "fractional arithmetic derivative" doesn't actually make sense. It fails to meet the basic decideratum of corresponding with an iterated arithmetic derivative. E.g., consider that 225″ = (225′)′ = ((3²·5²)′)′ = (2·3·5² + 3²·2·5)′ = (150 + 90)′ = 240′ = (2⁴·3·5)′ = 4·2³·3·5 + 2⁴·5 + 2⁴·3 = 480 + 80 + 48 = 608. Whereas, under the proposed definition we would allegedly equivalently have 225⁽²⁾ = (2!·3⁰·5² + 3²·2!·5⁰) = 50 + 18 = 68. I apologize to anyone who read the original post (??) who was thereby misled. The original post follows (with the erroneous section struck through).]

Wikipedia informs us of the idea of an arithmetic derivative—personally, I think this is a terrible name because it doesn't seem to be a rate of change of anything, but the motivation is clear enough, so let's go with it. It's a function on the natural numbers which we'll denote with the prime mark (" ′ "—the name of this symbol is not to be confused with the name for positive integers with exactly two divisors, which are also of—forgive me—"prime" importance in this discussion). It works like this: 0′ is 0, 1′ is 0, p′ is 1 for any prime number p, and the composite numbers get filled in with the product rule (ab)′ = a′b + ab′ (hence the "derivative" moniker).

For prime powers, the product rule degenerates into a power rule:

$$(p^a)' = \sum_{j:=1}^{a} 1 \cdot p^{a-1} = ap^{a-1}$$

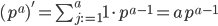
And this in turn makes it easy to compute the arithmetic derivative in general. Say that n∈ℕ has the prime factorization Π_i p_i^a_i. Then—

$$n' = \sum_{i} a_{i}p_{i}^{a_{i}-1} \prod_{j:\neq i} p_{j}^{a_{j}} = \sum_{i} a_{i}\frac{n}{p_{i}} = n \sum_{i} \frac{a_{i}}{p_{i}}$$

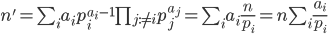
Arithmetic derivatives for small natural numbers are given as sequence A003415 in the Online Encyclopedia of Integer Sequences.

Some generalizations of this arithmetic derivative idea are discussed online (e.g., they say you can extend it to rational numbers using the familiar quotient rule), but (to my surprise) I didn't see any mentions of the obviously compelling idea of a fractional arithmetic derivative (in analogy to the fractional calculus). Repeated applications of the power rule for a prime power give us

$$(p^{a})^{(k)} = \frac{a!}{(a-k)!}p^{a-k}$$

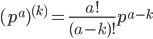
where the superscript parenthetical k indicates the kth arithmetic derivative for natural number k. But then if we just swap out those factorials for their gamma-function equivalents, we should have a qth power rule for real q—

$$(p^{a})^{(q)} = \frac{\Gamma(a+1)}{\Gamma(a-q+1)}p^{a-q}$$

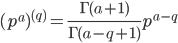
which in turn should give us a "fractional" qth arithmetic derivative for natural numbers:

$$n^{(q)} = \sum_{i} \frac{\Gamma(a_{i}+1)}{\Gamma(a_i-q+1)} \frac{n}{p_{i}^{q}}$$

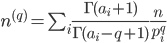
So this is a cute definition that seems to work, but what can we do with it? At time of writing I can only demur that further research is needed.