In the study of the elementary algebra, one occasionally hears of the conjugate roots theorem, which says that if z₀ is a root of a polynomial with real coefficients, then its complex conjugate is also a root. Or if you prefer, nonreal roots come in conjugate pairs. It also works in the other direction: if nonreal roots of a polynomial come in conjugate pairs, then the polynomial has real coefficients, because the purely imaginary parts cancel when you do the algebra: (x – (a + bi))(x – (a – bi)) = x² – x(a + bi) – x(a – bi) + (a² – (bi)²) = x² – 2ax + a² + b².

There's also this idea that conjugation is the unique nontrivial "well-behaved" automorphism on ℂ, a map from ℂ to itself that respects addition and multiplication: the sum (respectively product) of the conjugates is the conjugate of the sum (respectively product). The complex numbers are symmetrical around the real axis in a way that they're not around the imaginary axis: while i and –i are different from each other, you can't "tell which is which" because they behave the same way. Contrast to 1 and –1, which do behave differently: if someone put either 1 or –1 in a box, but they wouldn't tell you which, but they were willing to tell you that "The number in the box squares to itself," then you could figure out that the number in the box was 1, because –1 doesn't do that.

The existence of these two ideas (the conjugate roots theorem and conjugation-as-automorphism) can't possibly be a coincidence; there must be some sense in which nonreal roots of real-coefficient polynomials come in conjugate pairs because the polynomial "can't tell" "which is which". But it would be unsatisfying to just say this much and nothing more ("Theorem: That can't possibly be a coincidence. Proof ...??"); we want to say something much more general and precise. And in fact, we can—

Say that L is a field, and that K is a field that lives inside L, and that σ is a member of the group of field automorphisms of L that leave K alone (that is, map all members of K to themselves). Then we can show that

Theorem (generalized conjugate roots theorem). If z₀ is a root of a polynomial with coefficients in K, then σ(z₀) is too.

Proof. Let 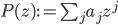$P(z) := \sum_j a_jz^{j}$ and suppose P(z₀) = 0. Then consider the value of P(σ(z₀)). Precisely because σ respects multiplication, we have 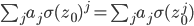$\sum_j a_j\sigma(z_{0})^{j} = \sum_j a_j\sigma(z_{0}^{j})$ and because σ doesn't disturb anything in K, that's the same as 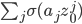$\sum_j \sigma(a_j z_{0}^{j})$ (because aσ(z) = σ(a)σ(z) = σ(az)), and because σ respects addition, that's also the same as 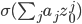$\sigma(\sum_j a_j z_{0}^{j})$. 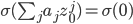But $\sigma(\sum_j a_j z_{0}^{j}) = \sigma(0)$, and σ(0) has to be zero for the automorphism to work. So P(σ(z₀)) is zero, but that's what I've been trying to tell you this entire time.