Earlier this year, Robert Hasner showed me something that I assume everyone else ("everyone else") already knows, but which I didn't know: every function on ℝ can be decomposed into the sum of an even function and an odd function—

$$f(x) = \frac{f(x)+f(-x)}{2} + \frac{f(x)-f(-x)}{2}$$

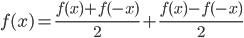
(In fact, as I later read elsewhere, there's nothing essentially twoful about this idea (at least, if you don't care about restricting yourself to ℝ): you can split a function into a sum of n functions f_j for j ∈ {0, ..., n–1} such that f_j(ωz) = ω^jf_j(z) where ω is an nth root of unity.)

I started seeing the same pattern in my reading, too. Like, every matrix can be decomposed into the sum of a symmetric and a skew-symmetric matrix:

A = ½(A + A^T) + ½(A – A^T)

(In fact, I have been given to understand that this observation is actually expressing a deep truth about the nature of linear transformations: every linear transformation is in some sense—which I hope to make more explicit later—the sum of a scaling in orthogonal directions (from the symmetric matrix; consider the spectral theorem) and a rotation (from the skew-symmetric matrix, which is said to represent an infinitesimal rotation).)

Also (and probably related to the matrix thing), in the geometric algebra, the geometric product of vectors can be expressed as the sum of an inner product and an anticommutative outer product.

Are there more examples of this theme of splitting something into symmetric and antisymmetric parts? Is there a general theorem explaining exactly which mathematical objects do this kind of thing?